Skip to contents

Computing area under the curve (AUC)

Source: vignettes/area-under-curve.Rmd
area-under-curve.Rmd

Model-free AUC

“Area under the curve” (AUC) is a measure of discounting that has the advantage of not assuming any underlying discount function ((Myerson et al., 2001)[https://doi.org/10.1901/jeab.2001.76-235]). If we have already computed indifference points, we can pass these directly to the AUC function:

data("td_ip_simulated_ptpt")
head(td_ip_simulated_ptpt)
#>   del    indiff
#> 1   3 0.9987226
#> 2   7 0.9866823
#> 3  20 0.9816838
#> 4  55 0.9489135
#> 5 148 0.8035958
#> 6 403 0.8001508
AUC(td_ip_simulated_ptpt)
#> [1] 0.1296151

However, if we only have choice-level data, we need to first compute indifference points. To do this, we can call td_bcnm() with discount_function = "model_free" (which fits an indifference point for each delay rather than computing indifference points based on a discount function) and then extract the indifference points in a dataframe using indiffs():

data("td_bc_single_ptpt")
indiff_mod <- td_bcnm(td_bc_single_ptpt, discount_function = 'model-free')
indiff_data <- indiffs(indiff_mod)
head(indiff_data)
#>         del    indiff
#> 1    7.0000 1.0000000
#> 2   30.4167 0.7582115
#> 3  182.5000 0.0847121
#> 4  730.5000 0.0000000
#> 5 3652.5000 0.0000000
AUC(indiff_data)
#> [1] 0.03146756

For the AUC computed this way, the later indifference points tend to have an outsize influence on the overall measure. To address this, Borges et al. (2016) suggest transforming the delays to a log or ordinal scale. These are implemented in the del_transform argument to AUC():

AUC(indiff_data, del_transform = 'log')
#> [1] 0.4978852
AUC(indiff_data, del_transform = 'ord')
#> [1] 0.4685847

Note that the area under the curve is always computed starting from delay 0, where an indifference point of 1 is assumed.

Model-based AUC

AUC can also be useful as a non-parametric measure of discounting that allows comparisons across different discount functions. The “model-based AUC” is computed by integrating the curve produced by a discount function (Gilroy & Hantula, 2018). To compute the model-based AUC, we first need to fit a model that uses a discount function and then call AUC() on that model:

data("td_bc_single_ptpt")
mod <- td_bcnm(td_bc_single_ptpt, discount_function = 'hyperbolic')
AUC(mod)
#> [1] 0.06592175

We can use the max_del acgument to integrate only up to a certain delay, in case maximum delays differ between participants:

AUC(mod, max_del = 1000)
#> [1] 0.1681596

As with the model-free AUC, we can transform the delays to a log scale. The ordinal transformation is not applicable here because it is not well-defined between points on the ordinal scale.

AUC(mod, del_transform = 'log')
#> [1] 0.5014776

Note that when del_transform = 'log', there is a subtle difference between calling AUC() on a table of indifference points and calling it on the “model-free” discount function: for a table of indiffernece points, indifference point interpolations are linear between transformed delays (illustrated in the first plot below). In contrast, for the model-free discount function, interpolations between indifference points are linear in the original scale of the data. This is evident in the curved interpolations in the second plot below:

# Linear in transformed scale:
plot(indiff ~ del, td_ip_simulated_ptpt, log = 'x', type = 'l', ylim = c(0, 1))
points(indiff ~ del, td_ip_simulated_ptpt)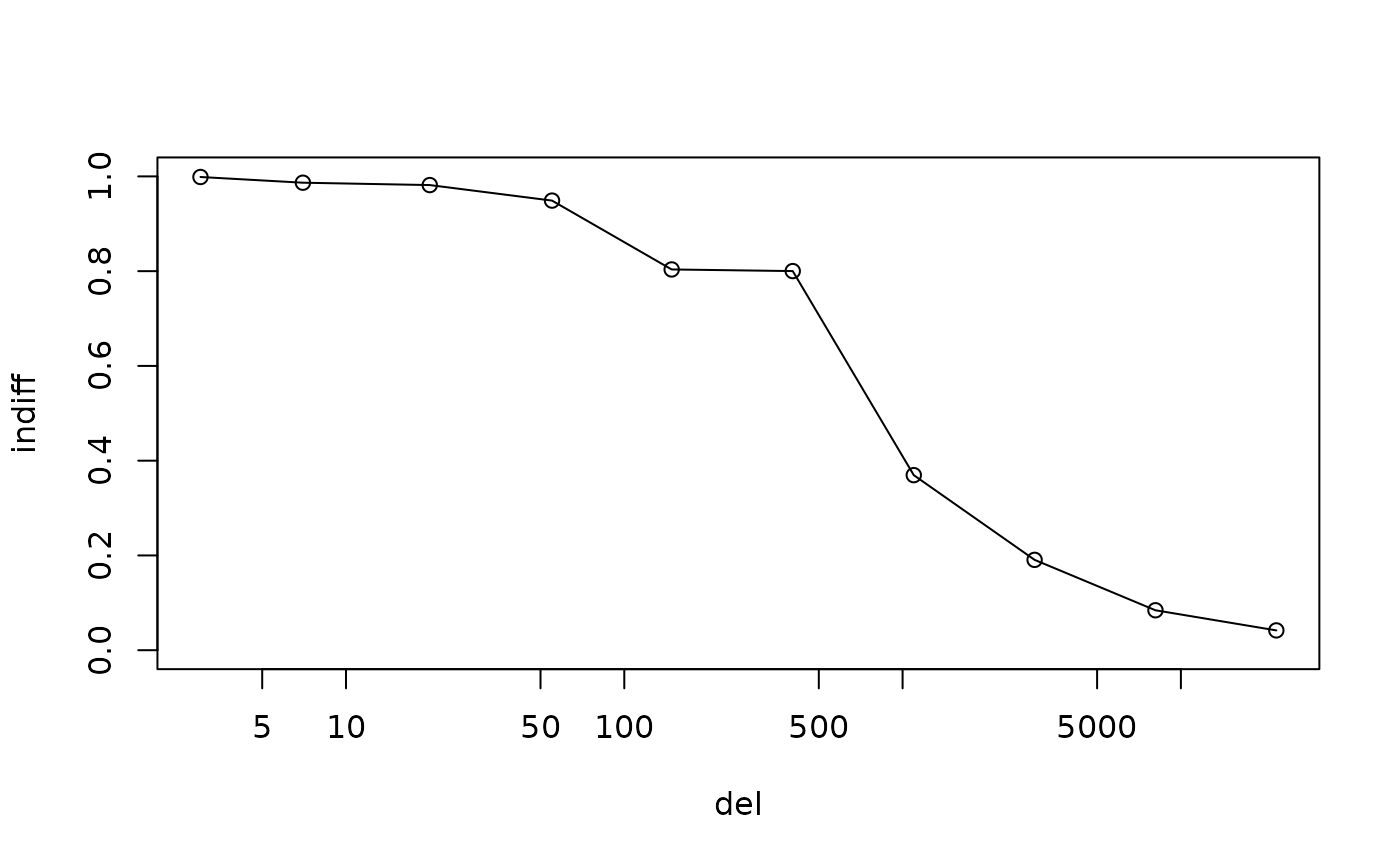

# Linear in original scale:
mod <- td_ipm(td_ip_simulated_ptpt, discount_function = 'model-free')
plot(mod, log = 'x', verbose = F)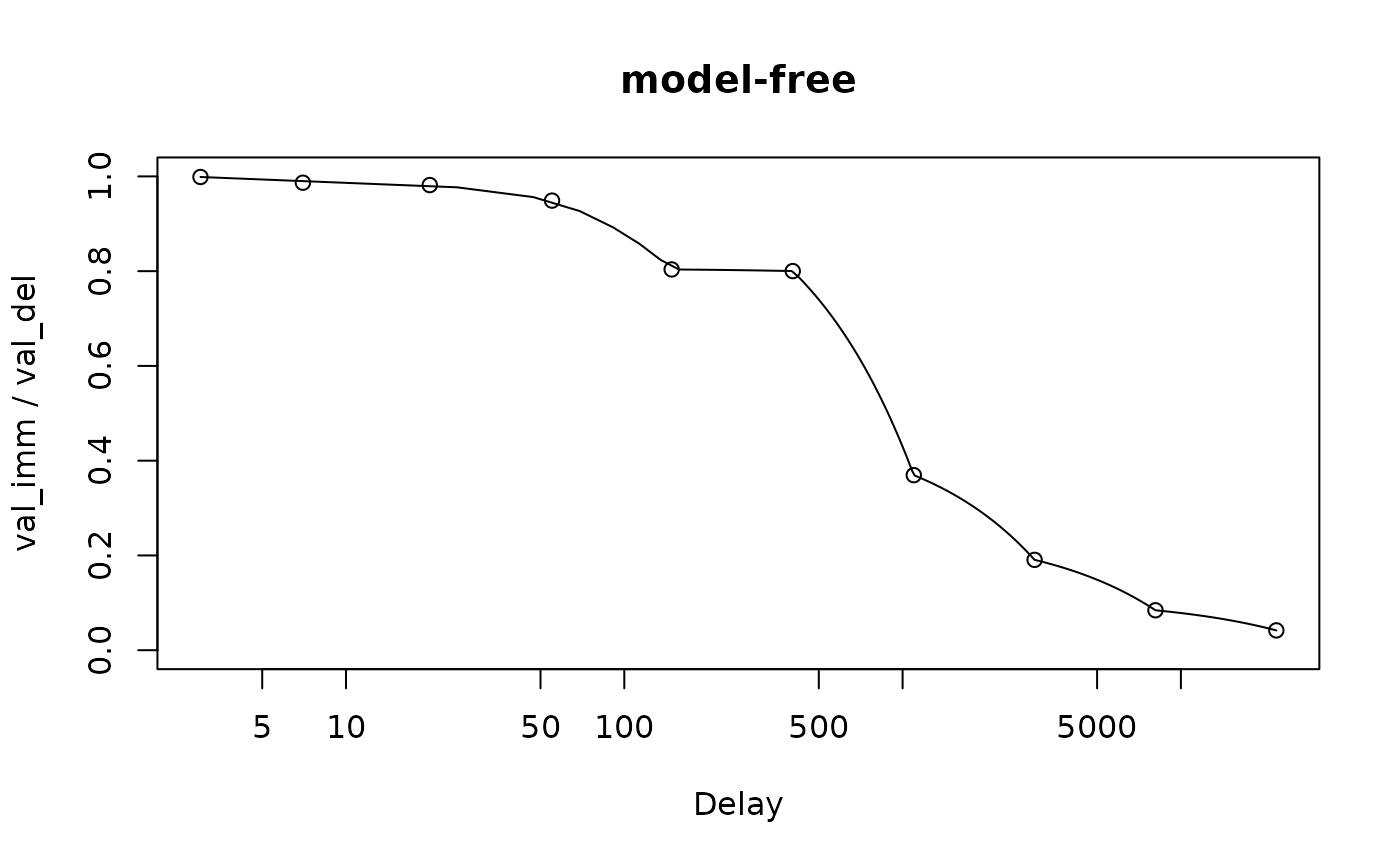

And indeed, the AUC calculations are slightly different:

AUC(td_ip_simulated_ptpt, del_transform = 'log')
#> [1] 0.669255
AUC(mod, del_transform = 'log')
#> [1] 0.6769932