Modeling binary choice data • tempodisco

library(tempodisco)

Classic methods

For binary choice data not explicitly designed to titrate out indifference points (as in an adjusting amount procedure), there are a few widely-used traditional scoring methods to quantify discounting.

Kirby scoring

One scoring method is the one designed for the Monetary Choice Questionnaire (Kirby, 1999):

data("td_bc_single_ptpt")
mod <- kirby_score(td_bc_single_ptpt)
print(mod)
#> 
#> Temporal discounting indifference point model
#> 
#> Discount function: hyperbolic, with coefficients:
#> 
#>          k 
#> 0.02176563 
#> 
#> ED50: 45.9439876371218
#> AUC: 0.0551987542147013

Although this method computes $k$ values according to the hyperbolic discount function, in principle it’s possible to use the exponential or power discount functions (though this is not an established practice and should be considered an experimental feature of tempodisco):

mod_exp <- kirby_score(td_bc_single_ptpt, discount_function = 'exponential')
print(mod_exp)
#> 
#> Temporal discounting indifference point model
#> 
#> Discount function: exponential, with coefficients:
#> 
#>           k 
#> 0.008170247 
#> 
#> ED50: 84.8379742026149
#> AUC: 0.0335100135964859
mod_pow <- kirby_score(td_bc_single_ptpt, discount_function = 'power')
print(mod_pow)
#> 
#> Temporal discounting indifference point model
#> 
#> Discount function: power, with coefficients:
#> 
#>         k 
#> 0.3052023 
#> 
#> ED50: 0.235591893994806
#> AUC: 0.1173431135372

Wileyto scoring

It is also possible to use the logistic regression method of Wileyto et al. (2004), where we can solve for the $k$ value of the hyperbolic discount function in terms of the regression coefficients:

mod <- wileyto_score(td_bc_single_ptpt)
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
print(mod)
#> 
#> Temporal discounting binary choice linear model
#> 
#> Discount function: hyperbolic from model hyperbolic.1, with coefficients:
#> 
#>          k 
#> 0.04372626 
#> 
#> Call:  glm(formula = fml, family = binomial(link = "logit"), data = data)
#> 
#> Coefficients:
#>     .B1      .B2  
#> 0.49900  0.02182  
#> 
#> Degrees of Freedom: 70 Total (i.e. Null);  68 Residual
#> Null Deviance:       97.04 
#> Residual Deviance: 37.47     AIC: 41.47

Newer methods

Linear models

The Wileyto et al. (2004) approach turns out to be possible for other discount functions as well (Kinley, Oluwasola & Becker, 2025.):

Name	Discount function	Linear predictor	Parameters
`hyperbolic.1`	Hyperbolic (Mazur, 1987): $\frac{1}{1 + kt}$	$\beta_1 \left(1 - \frac{v_D}{v_I} \right) + \beta_2 t$	$k = \frac{\beta_2}{\beta_1}$
`hyperbolic.2`	(Mazur, 1987): $\frac{1}{1 + kt}$	$\beta_1\left( \sigma^{-1}\left[\frac{v_\mathcal{I}}{v_\mathcal{D}}\right] + \log t \right) + \beta_2$	$k = e^\frac{\beta_2}{\beta_1}$
`exponential.1`	Exponential (Samuelson, 1937): $e^{-kt}$	$\beta_1 \log \frac{v_I}{v_D} + \beta_2 t$	$k = \frac{\beta_2}{\beta_1}$
`exponential.2`	Exponential (Samuelson, 1937): $e^{-kt}$	$\beta_1\left( G^{-1}\left[\frac{v_\mathcal{I}}{v_\mathcal{D}}\right] + \log t \right) + \beta_2$	$k = e^\frac{\beta_2}{\beta_1}$
`power`	Power (Harvey, 1986): $\frac{1}{(1 + t)^k}$	$\beta_1 \log \frac{v_I}{v_D} + \beta_2 \log (1 + t)$	$k = \frac{\beta_2}{\beta_1}$
`scaled-exponential`	Scaled exponential (beta-delta; Laibson, 1997): $w e^{-kt}$	$\beta_1\log\frac{v_{I}}{v_{D}} + \beta_2 t + \beta_3$	$k = \frac{\beta_2}{\beta_1}$ , $w = e^{-\frac{\beta_3}{\beta_1}}$
`nonlinear-time-hyperbolic`	Nonlinear-time hyperbolic (Rachlin, 2006): $\frac{1}{1 + k t^s}$	$\beta_1 \sigma^{-1}\left[\frac{v_{I}}{v_{D}}\right] + \beta_2\log t + \beta_3$	$k = e^\frac{\beta_3}{\beta_1}$ , $s = \frac{\beta_2}{\beta_1}$
`nonlinear-time-exponential`	Nonlinear-time exponential (Ebert & Prelec, 2007): $e^{-kt^s}$	$\beta_1 G^{-1}\left[\frac{v_\mathcal{I}}{v_\mathcal{D}}\right] + \beta_2\log t + \beta_3$	$k = e^\frac{\beta_3}{\beta_1}$ , $s = \frac{\beta_2}{\beta_1}$

Where $\sigma^{-1}[\cdot]$ is the logit function, or the quantile function of a standard logistic distribution, and $G^{-1}[\cdot]$ is the quantile function of a standard Gumbel distribution.

We can test all of these and select the best according to the Bayesian Information Criterion as follows:

mod <- td_bclm(td_bc_single_ptpt, model = 'all')
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
print(mod)
#> 
#> Temporal discounting binary choice linear model
#> 
#> Discount function: exponential from model exponential.2, with coefficients:
#> 
#>          k 
#> 0.01003216 
#> 
#> Call:  glm(formula = fml, family = binomial(link = "logit"), data = data)
#> 
#> Coefficients:
#>     .B1      .B2  
#>   3.597  -16.553  
#> 
#> Degrees of Freedom: 70 Total (i.e. Null);  68 Residual
#> Null Deviance:       97.04 
#> Residual Deviance: 15.7  AIC: 19.7

Nonlinear models

To explore a wider range of discount functions, we can fit a nonlinear model by calling td_bcnm. The full list of built-in discount functions is as follows:

Name	Functional form	Other names
`exponential` (Samuelson, 1937)	$f(t; k) = e^{-k t}$
`scaled-exponential` (Laibson, 1997)	$f(t; k, w) = w e^{-k t}$	Quasi-hyperbolic; beta-delta
`nonlinear-time-exponential` (Ebert & Prelec, 2007)	$f(t; k, s) = e^{-k t^s}$	Constant sensitivity
`dual-systems-exponential` (Ven den Bos & McClure, 2013)	$f(t; k_1, k_2, w) = w e^{-k_1 t} + (1 - w) e^{-k_2 t}$
`inverse-q-exponential` (Green & Myerson, 2004)	$f(t; k, s) = \frac{1}{(1 + k t)^s}$	Generalized hyperbolic (Loewenstin & Prelec); hyperboloid (Green & Myerson, 2004); q-exponential (Han & Takahashi, 2012)
`hyperbolic` (Mazur, 1987)	$f(t; k) = \frac{1}{1 + kt}$
`nonlinear-time-hyperbolic` (Rachlin, 2006)	$f(t; k, s) = \frac{1}{1 + k t^s}$	Power-function (Rachlin, 2006)
`power` (Harvey, 1986)	$f(t; k) = \frac{1}{(1 + t)^k}$

mod <- td_bcnm(td_bc_single_ptpt, discount_function = 'all')
print(mod)
#> 
#> Temporal discounting binary choice model
#> 
#> Discount function: exponential, with coefficients:
#> 
#>          k      gamma 
#> 0.01083049 0.09341821 
#> 
#> Config:
#>  noise_dist: logis
#>  gamma_scale: linear
#>  transform: identity
#> 
#> ED50: 63.9996305466619
#> AUC: 0.0252791100912786
#> BIC: 25.9537097154224

Choice rules

Several additional arguments can be used to customize the model. For example, we can use different choice rules—the “logistic” choice rule is the default, but the “probit” and “power” choice rules are also available (see this tutorial for more details):

# Probit choice rule:
mod <- td_bcnm(td_bc_single_ptpt, discount_function = 'exponential', choice_rule = 'probit')
# Power choice rule:
mod <- td_bcnm(td_bc_single_ptpt, discount_function = 'exponential', choice_rule = 'power')

Error rates

It is also possible to fit an error rate $\epsilon$ that describes the probability of the participant making a response error (see Vincent, 2015). I.e.: $P(\text{imm}) = \epsilon + (1 - 2\epsilon) g^{-1}[\eta]$ where $P(\text{imm})$ is the probability of choosing the immediate reward, $g$ is the link function, and $\eta$ is the linear predictor.

data("td_bc_study")
# Select the second participant
second_ptpt_id <- unique(td_bc_study$id)[2]
df <- subset(td_bc_study, id == second_ptpt_id)
mod <- td_bcnm(df, discount_function = 'exponential', fit_err_rate = T)
plot(mod, type = 'endpoints', verbose = F)
lines(c(0, 1), c(0, 0), lty = 2)
lines(c(0, 1), c(1, 1), lty = 2)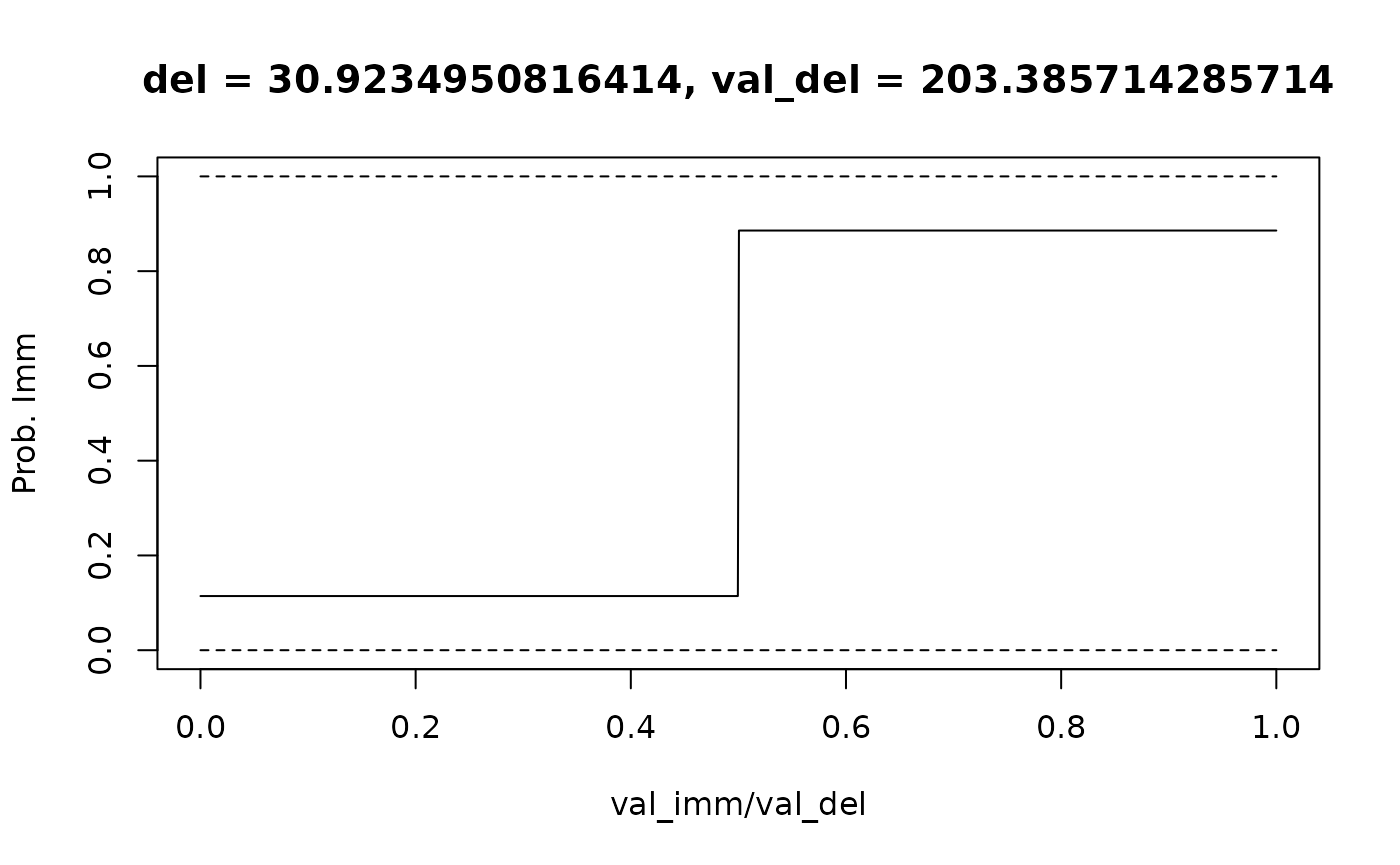

cat(sprintf("epsilon = %.2f\n", coef(mod)['eps']))
#> epsilon = 0.11

We can see that the probability of choosing the immediate reward doesn’t approach 0 or 1 but instead approaches a value of $\epsilon \approx 0.11$ .

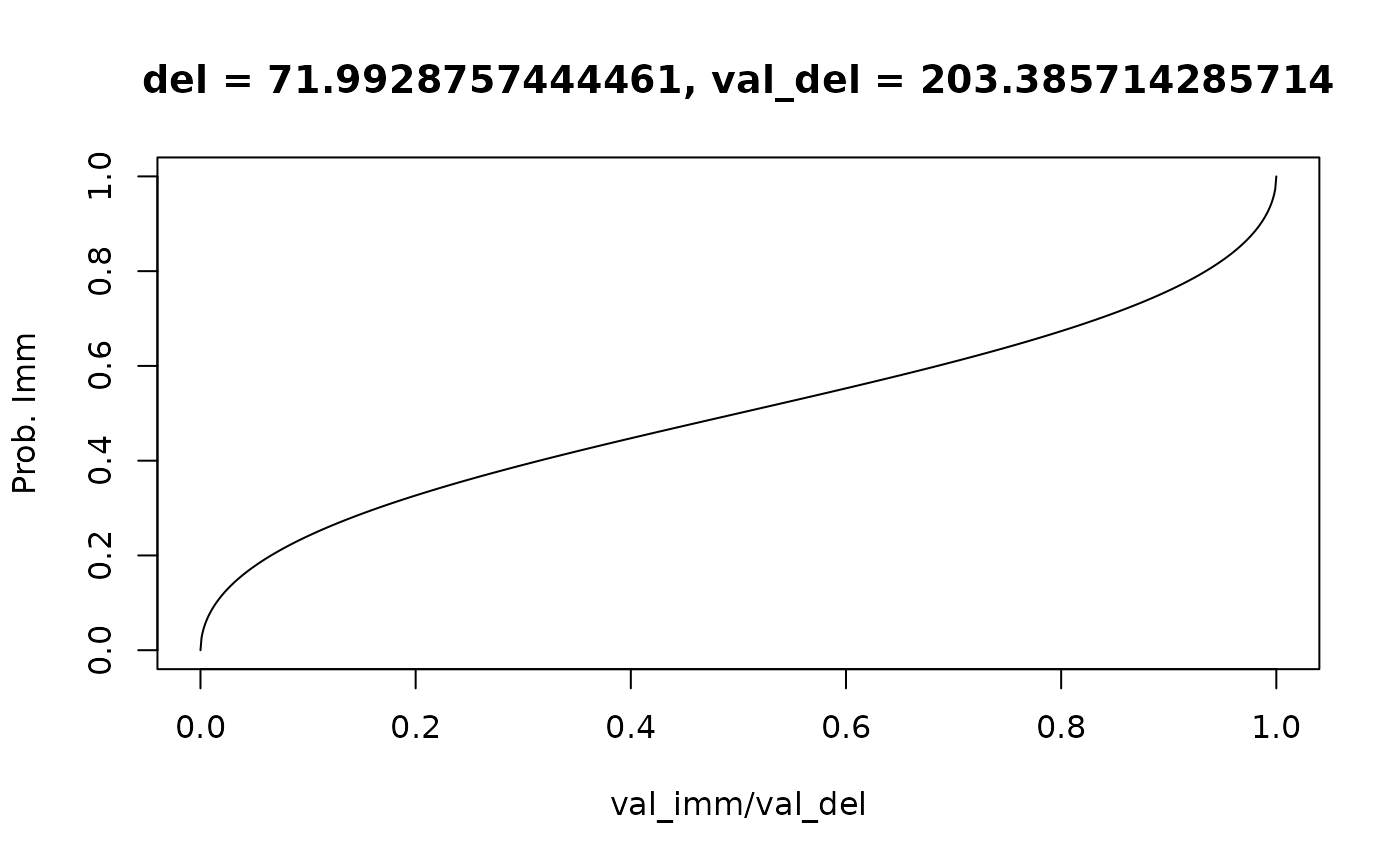
Fixed endpoints

Alternatively, we might expect that participants should never choose an immediate reward worth 0 and should never choose a delayed reward worth the same face amount as an immediate reward (Kinley, Oluwasola & Becker, 2025; see here for more details). We can control this by setting fixed_ends = T, which “fixes” the endpoints of the psychometric curve, where val_imm = 0 and val_imm = val_del, at 0 and 1, respectively:

mod <- td_bcnm(df, discount_function = 'exponential', fixed_ends = T)
plot(mod, type = 'endpoints', verbose = F, del = 50, val_del = 200)